Nga Ruben Avxhiu
Disa të dhëna që ju ndihmojnë për të kuptuar procesin.
Fituesi nuk është ai që merr më shumë vota në total, në gjithë Amerikën, por ai që mbledh më shumë prej të ashtuqaujturave Kolegje (Vota) Elektorale. Çdo shtet ka një numër të caktuar votash të tilla, të ndara në bazë të popullsisë. Sa më shumë njerëz ka shteti aq më shumë Kolegje Elektorale i takojnë. California, New York-u dhe Texasi kanë më shumë nga të gjitha.
Me pak përjashtime, kush del i pari në një shtet i merr të gjitha votat. Gjithësej po t’i mbledhësh janë 538 Kolegje Elektorale.
Që të zgjidhesh President duhet të marrësh të paktën 270 Kolegje Elektorale.
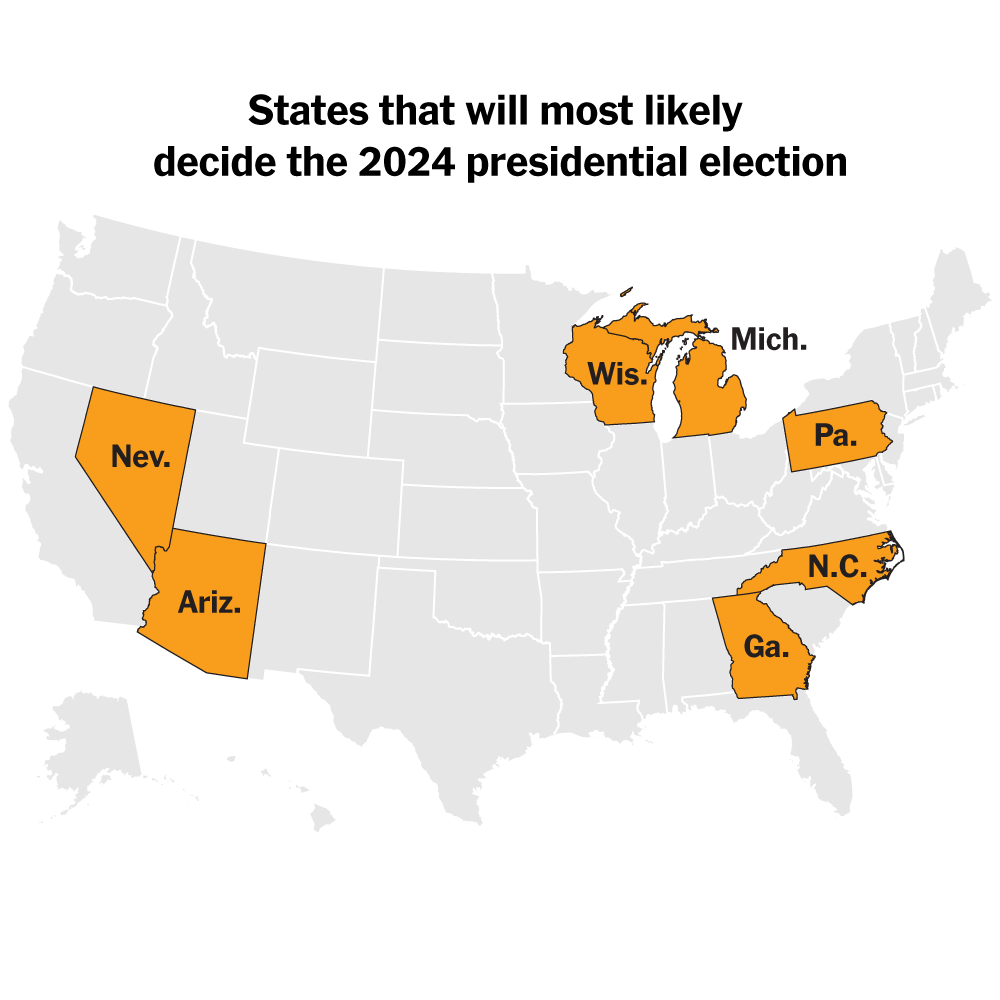
SHBA ka 50 shtete. Shumica e tyre dihet se për kë do të votojnë. Kështu që fushata është përqendruar kryesisht në 7 shtete. Aty do të ndahet shap nga sheqeri.
(Ka shqiptaro-amerikanë në të gjitha këto shtete, por sidomos në tre prej tyre: Michigan, Pennsylvania dhe Wisconsin.
Fushatat janë përqendruar më shumë në komunitetin e parë. Mesatarisht anketimet në Michigan i tregojnë kandidatët në distancë jo më shumë se 2% nga njëri-tjetri. Gabimi në anketime mund të shkojë 3%-5% dmth asgjë nuk mund të parashikohet me saktësi.
Shtetet e tjera ku mund të ketë të papritura janë: Nevada, North Carolina, Arizona, dhe Georgia. )
Statisticienët po bëjnë qejf me formula të ndryshme rezultatesh të mundshme, se rezultatet mund të kombinohen në shumë mënyra. Çfarë ndodhe nëse Trump fiton në Michigan dhe Pennsylvaia, por humbet në Wisconsin, Nevada, dhe Arizona? Çfarë ndodh nëse Harris fiton në Michigan, Wisconsin dhe Arizona por humbet në Pennsivlania, North Carolina, dhe Nevada?
Edhe ju mund të luani me numra të ndryshëm.
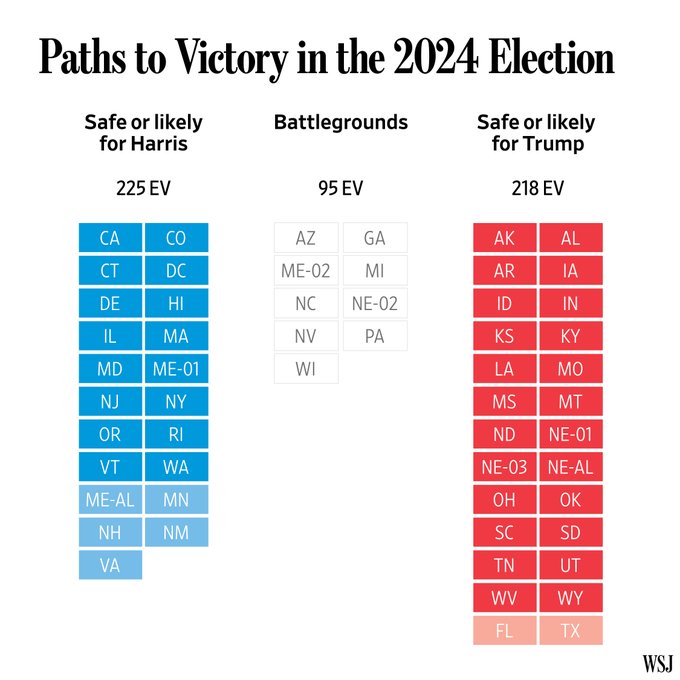
Nisuni nga kjo: Pa rezultatet në këto shtete dhe si dhe dy zona nga shtete që nuk ia japin të gjitha fituesit, Maine dhe Nebraska, rezultati është ky:
Kamala Harris 225
Donald Trump 218
Sipas WSJ, nga shtetet që kanë mbetur, Trump ka 32 kombinime rezultatesh, sipas të cilave mund të fitojë, kurse Harris vetëm 25.
Kamala Harris nga 25 kombinime rezultatesh, 48% kërkojnë që të dalë fituese në Pennsylvania.
Trump ka vërtet më shumë, 32, por në 81% të kombinimeve të mundshme, duhet të fitojë në Pennsylvania.
Pra sipas kësaj analize statistikore, Pennsylvania është shtet me më shumë rëndësi për kandidatin Trump sesa për demokraten Harris.
Tani, në Michigan, ku ndaj shqiptarëve është treguar më shumë interes nga fushatat. 52% e kombinimeve të mundshme të rezultateve në shtetet e pavendosura, përfshijnë një fitore për Harris në Michigan. Kurse për Trump 56%.
Pra, shteti Michigan ka rëndësi shumë për të dy, por pak më shumë për republikanin Trump.
Pak më ndryshe në Wisconsin. Fitorja në Wisconsin për Harris është në 56% të kombinimeve të ndryshme që mund të nxjerrin fituese të zgjedhjeve. Për Trump vetëm 47%.
E kështu me radhë.
Mund të bëni vetë llogari e kombinime të ndryshme, sidomos nëse jeni i fandaksur mbas statistikave.
Pennsylvania ka 19 Kolegje Elektorale
North Carolina 16
Georgia 16
Michigan 15
Arizona 11
Wisconsin 10
Nevada 6
Zonat Maine-02 dhe Nebraska-02 kanë nga 1 secila.
Pa këto rezultati është Harris-Trump 225-218. Ku do të shkojnë këto votat e mësipërme?
Ja një kombinim: Nëse fiton në North Carolina dhe Georgia, dy shtete shpesh të djathta, Trump ngjitet në 240 (218 + 16 + 16), pastaj i duhen vetëm 30.
I duhet mbase Pennsylvania që ka 19 dhe pastaj 10 Wisconsin dhe 1 nga Nebraska. Dhe Trump 270-Harris 268
Një kombinim i mundshëm për Harris është të fitojë Michigan dhe Arizona dhe shkon në 250 (225+15+10). Pastaj i duhen vetëm 20. Mbase fiton në Pennsylvania, dhe një kolegj e merr nga Maine. Ja u bë 270.
BARAZIM
A mund të dalin barazim? Gjithmonë bëhet kjo pyetje.
Po.
Nëse dalin barazim, votimi vazhdon në Kongres, në Dhomën e Përfaqësuesve, ku kongresistët nga secili prej 50 shteteve zgjedhin nga një kandidat.
Secili shtet deklaron se për kë votuan më shumë kongresistët e tij. Kush kap të paktën 26 shtete, fiton.
Barazimi nuk ka ndodhur kurrë, përveçse në filma, e seriale televizivë, por është statistikisht i mundshëm.
